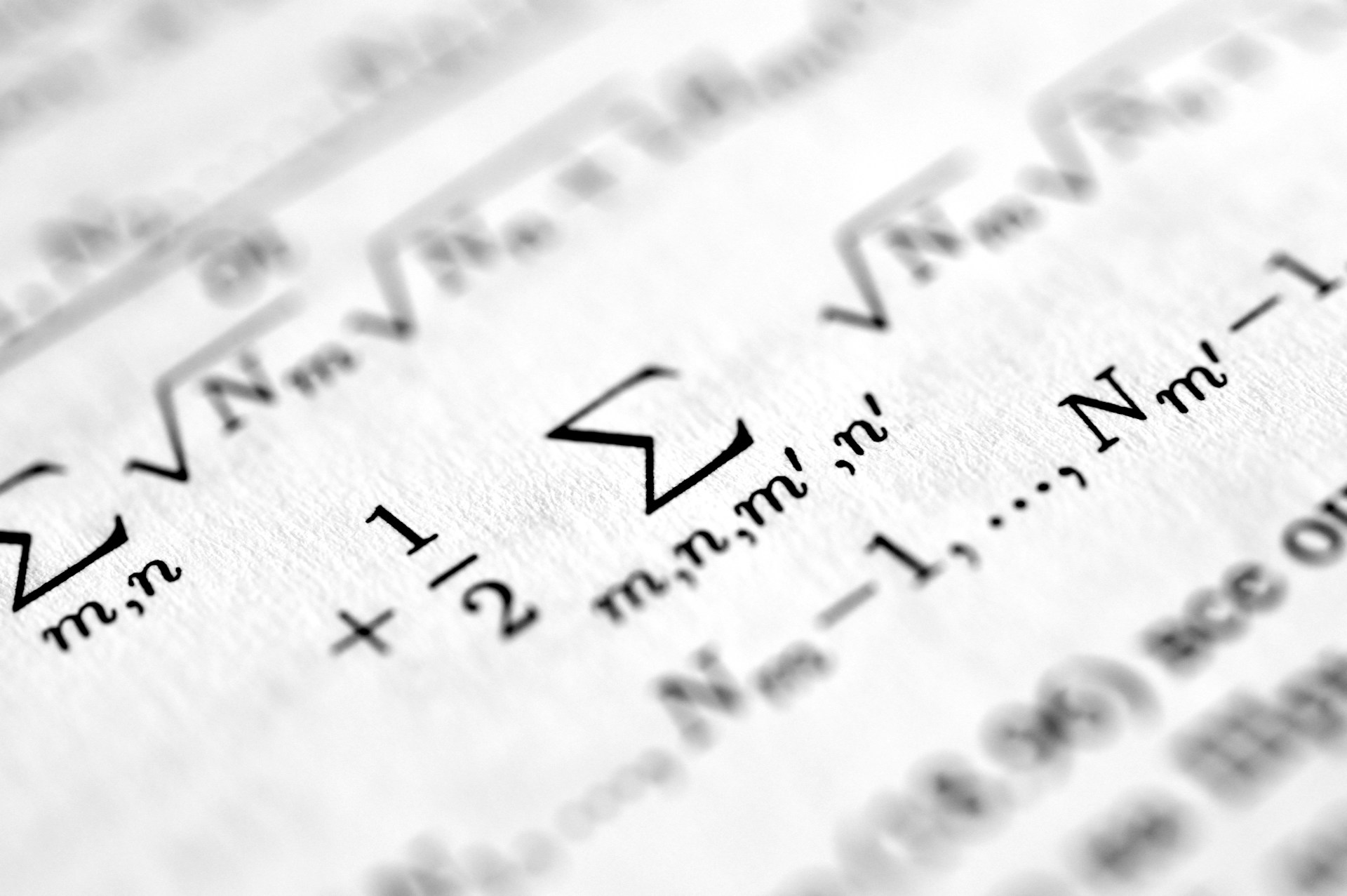บทนำ
สำหรับโจทย์ 5 ตัวเลขที่มีคำตอบเป้าหมายอยู่ระหว่าง 100-999 ซึ่งหลาย ๆ คนอาจจะไม่คุ้นกับการจะหาเลขใกล้เคียงในหลักร้อย
บทความนี้รวม สูตรและเทคนิคที่ต้องจำ ในสูตรเบื้องต้นที่จำได้ง่าย ๆ สำหรับทุก level:
- Level 1: ยกกำลัง (xn)
- Level 2: รากที่สอง ()
- Level 3: แฟกทอเรียล (n!) และซิกมา (∑)
พร้อมตารางสรุปว่า คำตอบเป้าหมายช่วงไหน ควรใช้สูตรอะไร
สารบัญ
- เทคนิคการแก้โจทย์: ค่าตั้งต้น ± เลขที่เหลือ
- สรุป: สูตรตามช่วงคำตอบเป้าหมาย
- Level 1: ยกกำลัง
- Level 2: รากที่สอง
- Level 3: แฟกทอเรียล
- Level 3 + ซิกมา
- Basic: บวก ลบ คูณ หาร
- คำถามที่พบบ่อย
เทคนิคการแก้โจทย์: ค่าตั้งต้น ± เลขที่เหลือ
วิธีคิด:
- พอเห็นคำตอบเป้าหมายปุ๊บ → ลองหาตัวเลขตั้งต้นที่มีค่าใกล้เคียงที่สุดก่อนเลย
- จากนั้น ลองใช้ตัวเลขบางตัวที่เรามีอยู่สร้างค่าตั้งต้นนั้นขึ้นมา
- สุดท้าย ก็เอาตัวเลขที่เหลือมาบวกหรือลบเพื่อปรับให้ได้ค่าตรงตามคำตอบเป้าหมาย
ตัวอย่าง: โจทย์ 12678 คำตอบ 727
- คำตอบ 727 ใกล้กับ 729 (36) → ต้องลบ 2
- สร้าง 36 จาก: ไม่มี 3 โดยตรง แต่ (8−6)=2 ไม่ได้… ลองใหม่
- ใช้ (8−6)=2 เป็นเลขฐาน, เลขชี้กำลังต้องได้ 9 → ไม่มี
- กลับมาใช้ 36: ต้องหา 3 และ 6 → (1+2)=3, 6 มีอยู่แล้ว!
- เหลือ 7, 8 → (8−6)=2 ❌ ไม่ใช่… ลองใหม่: 7 และ 8 → (8−7)=1 หรือ 8−6=2
- คำตอบ: 36−(8−6)=729−2=727 ✓
สรุป: สูตรตามช่วงคำตอบเป้าหมาย
| ช่วง | ยกกำลัง | แฟกทอเรียล | ซิกมา (เบื้องต้น) |
|---|
| 100-150 | 125, 128 | 120, 140, 144 | 105, 110, 120, 136, 140 |
| 150-250 | 216, 243 | 168, 180, 210, 240 | 156, 171, 204, 210, 231, 240 |
| 250-400 | 256, 343 | 252, 280, 315, 336, 360 | 272, 285, 300, 325, 342, 378, 385 |
| 400-600 | 512 | 420, 480, 504, 576, 600 | 385, 406, 420, 462, 465, 528 |
| 600-800 | 625, 729 | 630, 720 | 600, 630, 650, 666, 718, 719, 744, 756 |
| 800-999 | — | 840, 960 | 829, 840, 849, 851, 873, 879, 894, 903, 930 |
วิธีการที่ทำให้ได้แต่ละค่าอยู่ในหัวข้อด้านล่างเลย!
Level 1: ยกกำลัง (xn)
ท่าหลัก: ใช้การยกกำลังเพื่อสร้างตัวเลขให้มีค่าใกล้ ๆ กับคำตอบเป้าหมาย
ค่าตั้งต้นที่ต้องจำ
| ค่าตั้งต้น | สูตร |
|---|
| 125 | 53 |
| 128 | 27 |
| 216 | 63 |
| 243 | 35 |
| 256 | 28, 44 |
| 343 | 73 |
| 512 | 29, 83 |
| 625 | 54 |
| 729 | 36, 93 |
ตารางยกกำลัง
| เลขฐาน | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 9 | 27 | 81 | 243 | 729 | - | - | - | - |
| 4 | 16 | 64 | 256 | 1024 | - | - | - | - | - |
| 5 | 25 | 125 | 625 | - | - | - | - | - | - |
| 6 | 36 | 216 | 1296 | - | - | - | - | - | - |
| 7 | 49 | 343 | - | - | - | - | - | - | - |
| 8 | 64 | 512 | - | - | - | - | - | - | - |
| 9 | 81 | 729 | - | - | - | - | - | - | - |
| 10 | 100 | 1000 | - | - | - | - | - | - | - |
| 11 | 121 | 1331 | - | - | - | - | - | - | - |
| 12 | 144 | - | - | - | - | - | - | - | - |
| 13 | 169 | - | - | - | - | - | - | - | - |
| 14 | 196 | - | - | - | - | - | - | - | - |
| 15 | 225 | - | - | - | - | - | - | - | - |
ตารางกำลังสอง (x2)
ค่า x2 ที่อยู่ในช่วง 100-999:
| x | x2 | x | x2 | x | x2 |
|---|
| 10 | 100 | 18 | 324 | 26 | 676 |
| 11 | 121 | 19 | 361 | 27 | 729 |
| 12 | 144 | 20 | 400 | 28 | 784 |
| 13 | 169 | 21 | 441 | 29 | 841 |
| 14 | 196 | 22 | 484 | 30 | 900 |
| 15 | 225 | 23 | 529 | 31 | 961 |
| 16 | 256 | 24 | 576 | | |
| 17 | 289 | 25 | 625 | | |
ตัวอย่างโจทย์
| ตัวเลข | คำตอบ | สมการ |
|---|
| 02568 | 513 | 60+85−2=1+512=513 |
| 35613 | 181 | 1+336−5=4724=181 |
| 57037 | 378 | 5×7+73=35+343=378 |
| 23379 | 907 | (3+3×9)2+7=302+7=907 |
Level 2: รากที่สอง ()
ท่าหลัก: ใช้รากที่สองเพื่อสร้างตัวเลขใหม่ ๆ ขึ้นมาเป็นเลขฐานหรือเลขชี้กำลังเพิ่มเติม
Sqrt ที่ใช้บ่อยที่สุด
| สูตร | ค่า | ใช้ทำอะไร |
|---|
| 4 | 2 | เลขฐาน 2n, เลขชี้กำลัง x2 |
| 9 | 3 | เลขฐาน 3n, เลขชี้กำลัง x3 |
| 16 | 4 | เลขชี้กำลัง x4 |
| 25 | 5 | 5!=120 |
| 36 | 6 | 6!=720 |
ค่าตั้งต้นที่ต้องจำ (เพิ่มจาก Level 1)
| ค่าตั้งต้น | สูตร | ตัวอย่าง |
|---|
| 128 | (4)7 | (4)7+3=131 |
| 243 | (9)5 | (9)5−2=241 |
| 512 | (4)9 | (4)9+6=518 |
| 729 | (9)6 | (9)6−4=725 |
ตัวอย่างโจทย์
| โจทย์ | คำตอบ | สมการ |
|---|
| 14847 | 123 | (4)8−1−(7−4)=27−5=123 |
| 13169 | 732 | (1+3)+(9)6−1=4+729−1=732 |
| 24479 | 512 | (4)9+(7−4−4)=512+0=512 |
| 23469 | 185 | 2+9×((4)6−3)=2+3×61=185 |
Level 3: แฟกทอเรียล (n!)
ท่าหลัก: ใช้แฟกทอเรียลในการสร้างคำตอบเป้าหมาย — บอกเลยว่านี่เป็นท่าที่มีประโยชน์มากสำหรับโจทย์ 5 ตัวเลข!
ค่าตั้งต้นที่ต้องจำ
| 100-150 | 150-250 | 250-400 | 400-600 | 600-800 | 800-999 |
|---|
| 5!=120 | 4!×7=168 | 7!/20=252 | 7!/12=420 | 7!/8=630 | 5!+6!=840 |
| 7!/36=140 | 6!/4=180 | 7!/18=280 | 5!×4=480 | 6!=720 | 5!×8=960 |
| 3!×4!=144 | 7!/24=210 | 7!/16=315 | 7!/10=504 | | 5!×7=840 |
| 6!/3=240 | 7!/15=336 | 7!/9=560 | | 7!/6=840 |
| 5!×2=240 | 6!/2=360 | 4!×4!=576 | | |
| | 7!/14=360 | 5!×5=600 | | |
ตัวอย่างโจทย์
| โจทย์ | คำตอบ | สมการ |
|---|
| 01449 | 125 | (9−4)!+(1−0)×5=120+5=125 |
| 02346 | 720 | (2+4)!+0×3=6!=720 |
| 14478 | 728 | (7−1)!+(4+4)=720+8=728 |
| 11257 | 841 | 5!×7+1×1=840+1=841 |
| 36025 | 608 | 36−(5!+20)=729−121=608 |
Level 3 + ซิกมา (∑)
ท่าหลัก: ใช้ซิกมาสำหรับคำตอบเป้าหมายที่เทคนิคแฟกทอเรียลและยกกำลังเอาไม่อยู่ หรือทำแล้วยังไม่ได้ค่าที่ต้องการ
∑i (ผลบวก 1 ถึง n)
ขอบเขตบนที่ใช้บ่อย: 14 (2×7), 18 (3×6), 20 (4×5), 21 (3×7), 24 (4×6), 25 (5×5), 28 (4×7), 30 (5×6), 35 (5×7), 36 (6×6), 42 (6×7)
| 100-150 | 150-250 | 250-400 | 400-600 | 600-800 | 800-999 |
|---|
| ∑i=12×7i=105 | ∑i=13×6i=171 | ∑i=14×6i=300 | ∑i=14×7i=406 | ∑i=15×7i=630 | ∑i=16×7i=903 |
| ∑i=13×5i=120 | ∑i=14×5i=210 | ∑i=15×5i=325 | ∑i=15×6i=465 | ∑i=16×6i=666 | |
| ∑i=14×4i=136 | ∑i=13×7i=231 | ∑i=13×9i=378 | ∑i=14×8i=528 | | |
∑(i+i) (ผลบวก 2i)
| 100-150 | 150-250 | 250-400 | 400-600 | 600-800 | 800-999 |
|---|
| ∑i=12×5(i+i)=110 | ∑i=13×4(i+i)=156 | ∑i=14×4(i+i)=272 | ∑i=14×5(i+i)=420 | ∑i=14×6(i+i)=600 | ∑i=14×7(i+i)=812 |
| ∑i=12×7(i+i)=210 | ∑i=13×6(i+i)=342 | ∑i=13×7(i+i)=462 | ∑i=15×5(i+i)=650 | ∑i=15×6(i+i)=930 |
| ∑i=13×5(i+i)=240 | | | ∑i=13×9(i+i)=756 | |
∑(i×i) (ผลบวกกำลังสอง)
| 100-150 | 150-250 | 250-400 | 400-600 | 600-800 | 800-999 |
|---|
| ∑i=17(i×i)=140 | ∑i=18(i×i)=204 | ∑i=19(i×i)=285 | ∑i=12×5(i×i)=385 | ∑i=13×4(i×i)=650 | |
ซิกมากับแฟกทอเรียล
รูปแบบที่ใช้บ่อย:
| รูปแบบสมการในซิกมา | ขอบเขต | ผลลัพธ์ | หมายเหตุ |
|---|
| i+i! | (5, 6) | 851 | ใช้บ่อยมาก |
| i+i! | (4, 6) | 879 | |
| i+i! | (1, 6) | 894 | |
| i×i! | (1, 5) | 719 | |
| i×i! | (2, 5) | 718 | |
| i!−i | (5, 6) | 829 | |
| i!−i | (4, 6) | 849 | |
| (i+i)! | (1, 3) | 746 | =(2!)+(4!)+(6!)=2+24+720 |
| (i+i)! | (2, 3) | 744 | =(4!)+(6!)=24+720 |
| i! | (1, 6) | 873 | |
| i! | (5, 6) | 840 | =5!+6!=120+720 |
ตัวอย่างโจทย์
| โจทย์ | คำตอบ | สมการ |
|---|
| 12568 | 465 | ∑i=15×6i+(8−6−2×1)=465+0=465 |
| 05577 | 650 | ∑i=15×5(i+i)+(7−7)×0=650 |
| 33669 | 669 | ∑i=16×6i+(9−3−3)=666+3=669 |
| 13578 | 629 | ∑i=15×7i−(8−3−1−3)=630−1=629 |
| 24566 | 851 | ∑i=56(i+i!)+(4−2)×(6−6)=851+0=851 |
Basic: บวก ลบ คูณ หาร
สำหรับ Basic level ที่ใช้แค่ +, −, ×, ÷ นั้น ไม่มีสูตรตายตัว ต้องฝึกคิดด้วยตัวเอง!
ลำดับการลอง (ถ้าไม่รู้ level)
- ลองแฟกทอเรียลก่อนเลย — โดยเฉพาะถ้าในโจทย์มีเลข 5, 6, หรือ 9 → ให้รีบนำไปทำ 5!, 6!
- ลองยกกำลัง — ถ้าเห็นว่าคำตอบเป้าหมายมีค่าใกล้ ๆ กับ 128, 256, 512, 729 → ลองใช้ยกกำลังดู
- ลองซิกมา — ถ้าเจอคำตอบเป้าหมายหน้าตาแปลก ๆ อย่าง 300, 465, 666 → ลองนึกถึงซิกมา
- ลอง Basic — ถ้าลองมาทุกท่าแล้วยังไม่ได้จริง ๆ → กลับมาที่พื้นฐาน คือการหาตัวคูณที่ลงตัว
คำถามที่พบบ่อย (FAQ)
Level หรือ “ระดับ” ใน Fastmath คืออะไร?
| Level | เครื่องหมายที่ใช้ได้ |
|---|
| Basic | +, −, ×, ÷ |
| Level 1 | Basic + ยกกำลัง |
| Level 2 | Level 1 + ราก (ห้ามซ้อนกัน) |
| Level 3 | Level 2 + แฟกทอเรียล, ซิกมา (รากซ้อนได้ 2 ชั้น) |
กฎทั่วไป:
- คำตอบต้องเป็นจำนวนเต็มบวก
- ต้องใช้ตัวเลขจากโจทย์ให้ครบทุกตัว
- ห้ามนำตัวเลขมาต่อกันเป็นทศนิยมหรือจำนวนหลายหลัก
สามารถศึกษาเพิ่มเติมได้ที่ “ระดับ” ใน Fastmath คืออะไร?
ซิกมา (∑) คืออะไร?
ซิกมา หรือ ผลรวม (Summation) คือการบวกเลขตั้งแต่ค่าเริ่มต้นถึงค่าสิ้นสุด
ตัวอย่าง:
- ∑i=14i=1+2+3+4=10
- ∑i=23i2=22+32=4+9=13
- ∑i=23i!=2!+3!=2+6=8
สามารถศึกษาเกี่ยวซิกมาเพิ่มเติมได้ที่ ซิกมา คืออะไร?
แฟกทอเรียล (Factorial) คืออะไร?
แฟกทอเรียล (เครื่องหมาย !) คือการคูณเลขตั้งแต่ 1 ถึงตัวเลขนั้น
ตัวอย่าง:
- 3!=1×2×3=6
- 4!=1×2×3×4=24
- 5!=1×2×3×4×5=120
- 6!=720
กรณีพิเศษ: 0!=1 (ตามนิยามทางคณิตศาสตร์)
สามารถศึกษาเกี่ยวแฟกทอเรียลเพิ่มเติมได้ที่ แฟกทอเรียล คืออะไร?
อย่าลืมติดตามพวกเราใน Facebook!